El teorema de Pitágoras, no se puede demostrar en el triangulo obtusángulo debido a que la condición necesaria para que se de la proporción en que sea rectángulo. Por eso, tiene mas de 90º al ángulo en cuestión, aplicando la formula de las «Desigualdades de Pitágoras», en las que no se cumple, como manera de de determinar el mismo tamaño de ese: a^2+b^2< c^2 (ya que el lado opuesto es mayor), por lo que no se mantiene la igualdad del Teorema.
De ese modo, si tuviéramos 5^2+6^2= c=2, tendría que ser siempre menor a sus cuadrados. Por tanto, 25+36=C^2, de modo que quedaría que eso resulta 61 = c^2, aunque sin embargo C=9, de modo que se vería que no se puede continuar porque evidente que 61 no es igual a 81. De forma, que lo que quedaría es que a^2+b^2< c^2, demostrando como en esta ocasión estamos ante triangulo obtusángulo, ya que la hipotenusa es el ángulo de mayor grado.
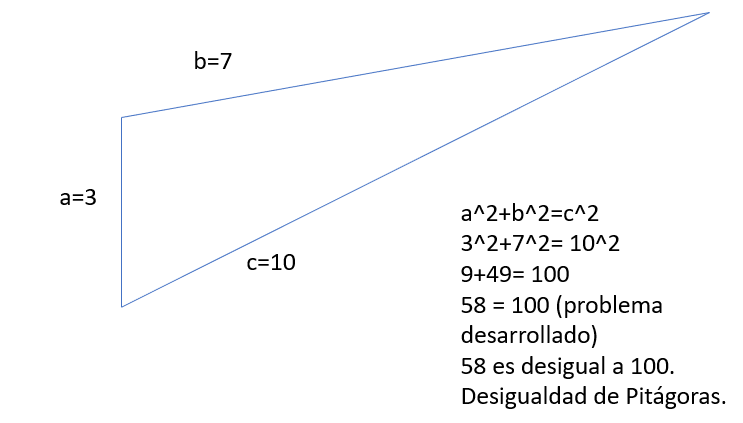
Tomando otro ejemplo, supón que el cateto a(3) y b (7) al cuadrado todos suman 9+49=58, pero que la hipotenusa es 10^2. El problema en este caso, es que no se podría realizar la igualdad del teorema de Pitágoras (a^2+b^2=c^2), ya que el cuadrado resultante de 10 sería 100 casi doblando la suma de los 1ros 2 catetos. De modo, que aquí se mostraría otro ejemplo de como no se respetaría el principio de igualdad, ya que el obtusángulo es bastante más grande.