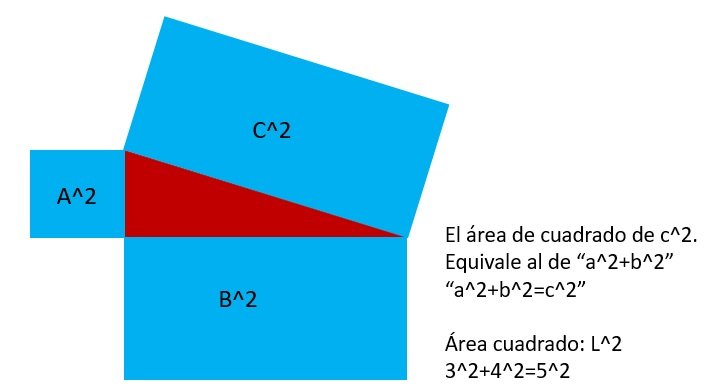
A día de hoy, vamos a demostrar de manera geométrica, el teorema de Pitágoras. Empleando la formula de los cuadrados, se puede ver como en realidad las proporciones del mismo, darían con que de otra forma, «no triangular», se cumplen las especificaciones que aparecen reflejadas en este principio matemático de hace 2000 años mínimo de antigüedad. Por eso, es lo que se pretende que sea la explicación de lo que vas a aprender hoy, en este articulo.
Si a cada lado del triangulo, se le pusiera cuadrados sobre ello, quedaría como la forma algo alterada. Lo curioso, es que el área del cuadrado «l^2», coincide con la formula del teorema de Pitágoras. De modo, que si al lado pequeño, 3^2 (a) +4^2 (b) =5^2 (c), resultaría que la proporción del teorema en cuestión se respetaría, lo que seria demostración a la vez de forma geométrica, ya que coincide con la formula de los lados del cuadrado, que se enseña.