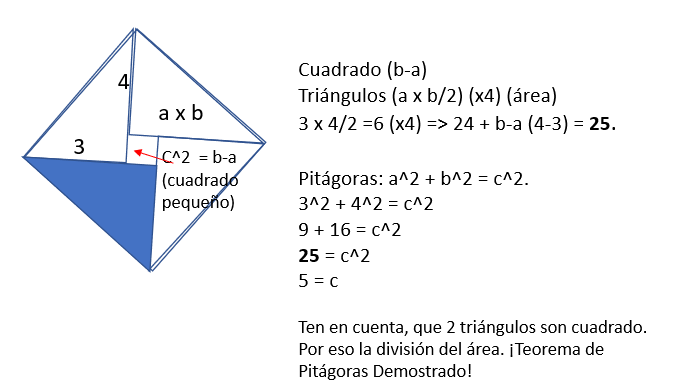
La demostración del teorema de Pitágoras china, es sin duda más que visual ya que emplea triángulos con formas dentro de él, para representar la proporción matemática. Esta datado del año 500-300 a.c, de modo que es poco probable que se conociera, por Pitágoras, escrito en el Zhoubi Suanjing, cuyo autor se cree que es chinos de la dinastía de Han, de manera que se puede estudiar de forma mas que profunda. Así, que vamos a ello con la explicación.
Dibujando 4 triángulos de lado (a+b), dentro de cuadrado quedaría de forma que encajara casi perfecto, salvo porque quedaría dentro de ello pequeño cuadrado entre lo que falta, de nombre c^2. Por lo tanto, habría que aplicar la formula del cuadrado (a x b /2) por 4, con tal de sacar el el área de ellos, a fin de saber su proporción. (3 x 4 /2 = 6), que multiplicado por los 4 lados, sería 24. Aplicando, la formula de ese cuadrado de b-a (c^2), de modo que sería 4-3 =1.
¿Cuál es la gracia de esto? Resultado, que se cogemos a^2 + b^2 = c^2, sería 3^2 + 4^2 = c^2, dando 9 + 16 =c^2, siendo 25 = c^2, que es 5 = C. Lo importante, es que ese 25 es el general de los lados, que teniendo en cuenta el anterior 24 + el cuadrado (b-a =1), sería también 25. De modo, que aplicándolo de esa manera, se puede puede llegar a la demostración, con triángulos, a la manera china como el teorema de Pitágoras es posible, puesto que se llega al mismo resultado.