El teorema de Pitágoras tiene varias maneras de probarse, como se demostró en la India en el S. XII gracias a ejemplo que usaba cuadrados con los que se veía como las proporciones de los lados daba con la formula del mismo. Por eso, aquí el objetivo es demostrarte como a través de este método también se puede hacer los cálculos de la operación. Así, que aquí presentamos la demostración aplicando la idea de Bashkara, que es sencilla de amera visual.
Aquí te mostramos la demostración basada en la idea de Bhaskara, que es sencilla y visual. Dibujamos un cuadrado grande de lado a+ba + ba+b, y colocamos dentro de él cuatro triángulos rectángulos con lados a, b y c. Si los organizamos correctamente, queda en el centro un cuadrado más pequeño con lado c, que se forma al juntar las hipotenusas. Por lo que en realidad, estarías a punto de tenerlo, ya que es necesario aplicar la formula del área.
El área del cuadrado grande se puede calcular de dos maneras:
- Como un solo cuadrado: (a+b)2
- Como la suma de las áreas de 4 triángulos y el cuadrado central: 4⋅(2/1ab)+c2=2ab+c2
Igualamos las dos formas de calcular el área: (a+b)2=2ab+c2
Desarrollamos el cuadrado: a2+2ab+b2=2ab+c2
Restamos 2ab a ambos lados:
a2+b2=c2
¡Y así se demuestra el teorema de Pitágoras de forma visual y sencilla!
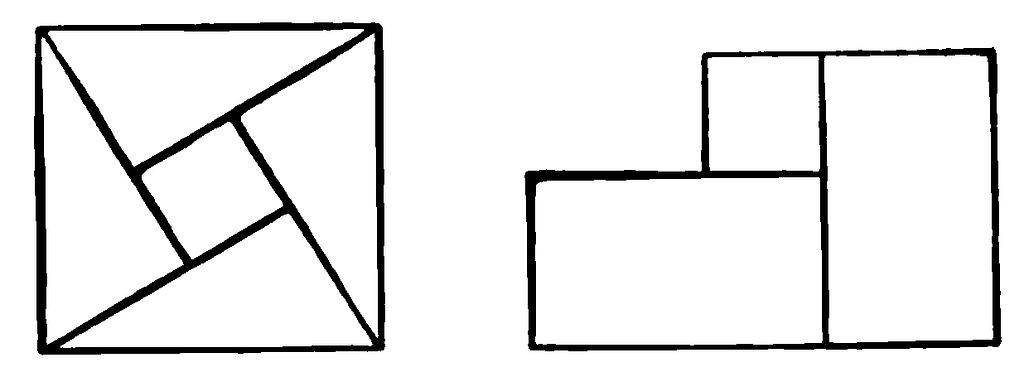
De manera que esta formula queda: 4 x (ab/2) +c^2 = ab^2 +c^2 –> a^2+ b^2 +2ab +c^2 = 2ab +c^2 –> a^2+b^2 = c^2.
.