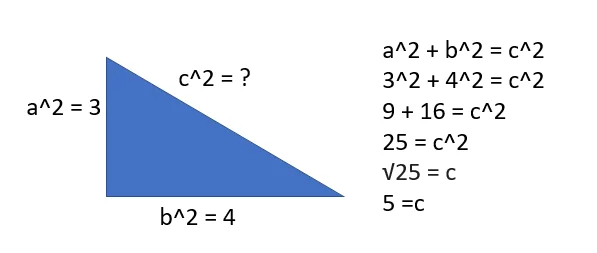El teorema de Pitágoras, es complejo ya que se puede demostrar de varias maneras como se cumple su formula en múltiples ocasiones. De modo, que esta entrada esta pensada para probar como también puede comprobarse de forma aritmética, el problema matemático. Así, que los próximos párrafos estarán dedicados a explicarlo en detalle, paso a paso, para que quede bien claro como sería la manera de llegar a la demostración del mismo. ¡Ahora vamos!
Para ello, tendríamos que usar la formula habitual del teorema, (a^2 + b^2 = c^2), de manera que se le asigne valores a cada letra, como (a=3 y b=4), de modo que al hacer los cálculos quedaría que (9 + 12 = c^2), siendo (25 = c^2), de modo que (√25 = c) , así que, (c=5). De modo que aplicando la formula se vería, como se cumple la proporción del teorema de Pitágoras con este ejemplo, viendo como en esta es posible obtener la demostración del teorema aritmética.
En caso de que haya alguna duda, vamos a probar con otros números, siendo (a^2 + b^2 = c^2), en realidad (a=5 y b=12), de manera que al pasarlo a la formula del teorema, quedaría de este modo (5^2 + 12^2 = c^2), puesto que dejaría el resultado de (25 + 144 = c^2), tendría a ser (169 = c^2), pues resolviendo (√169 = c), dejando el resultado de (13=c), por lo que aquí se cumpliría de nuevo. Así, que esta es otra manera de mostrar el teorema de Pitágoras de forma aritmética.