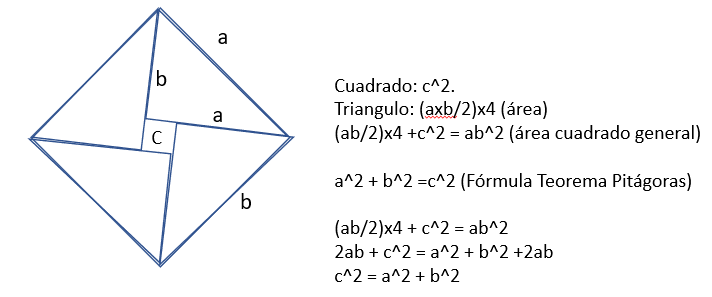
La demostración del teorema de Pitágoras, es otra manera de comprobar que las proporciones que dan la formula se cumple sin importar en que manera se represente, ya que acaba siendo evidente que acaba por mantenerse. En este caso, se trata de la demostración algebraica, usando áreas, formulas y cuadrados con los que ver como es verídico. De esta manera, esperamos que este articulo, se haga lo más ameno, sencillo y comprensible posible.
Es necesario, empezar dibujando 4 triángulos que dejen en medio del todo cuadrado pequeño llamado «c», de este modo se podría decir que ese cuadrado «a+b» (desigual en lados), se podría traducir por la formula 4xab/2 (área triángulo)+ c^2 (área cuadrado), de modo que al resolverla quedaría que «a+b»^2 = 2ab +c^2, de modo que esto seria a+b^2 = 2ab+ c^2, siendo a^2 + b^2 +2ab = 2ab + c^2, que eliminando los iguales quedaría a^2 + b^2 = c^2 de resultado.